This is joint work by Théis Bazin, Gaëtan Hadjeres, Philippe Esling and Mikhail Malt, published at the 2020 Joint Conference on AI Music Creativity.
Here is a video demo of the resulting tool, NOTONO, where we use it to interactively transform sounds (taken from the NSynth dataset) which we then assemble in Ableton Live to create a simple Techno song:
In this paper, we adapt the VQ-VAE-2 architecture to the interactive generation of sounds.
To this end, we introduce a modified version of the Mel-IF representation proposed in the GANSynth paper, that allows to remove irrelevant noise in this representation, making it more adapted to quantization via the VQ-VAE-2.
We then follow the approach proposed in the original VQ-VAE-2 paper and generate new sounds by sampling from the distribution of codemaps produced by the trained VQ-VAE-2. This has the advantage of turning the intractable autoregressive modeling of full-scaled \( 1024 \times 128 \), real-valued spectrograms into just sampling two small discrete codemaps of sizes \( 32 \times 4 \) and \( 64 \times 8 \).
Table of content
- VQ-VAE-2 Architecture
- Image-like Representation for Audio
- Sequence-masked Transformers for Inpainting
- Experiments
VQ-VAE-2 Architecture
The VQ-VAE-2 is a two-layer hierarchical model based on the common VAE encoder-decoder framework and was originally introduced for the generation of images. This model learns to encode 2D images onto two, 2D integer arrays of query indexes: the top codemap and the bottom codemap.
This quantization to integers is performed by learning within each of the two quantized layers a dictionary of code vectors onto which the latent encoder representations are projected. These two codemaps are conditionally bound. Indeed, the encoder of the VQ-VAE-2 first downsamples and quantizes the input image into the bottom map. This first representation is then further downsampled and again quantized, yielding the top codemap.
In the decoder, the top codemap is first reconstructed using the code vectors of the learned dictionary. This reconstruction is then used as a conditioning information for the decoding of the bottom codemap.
This architecture is represented in the following diagram.
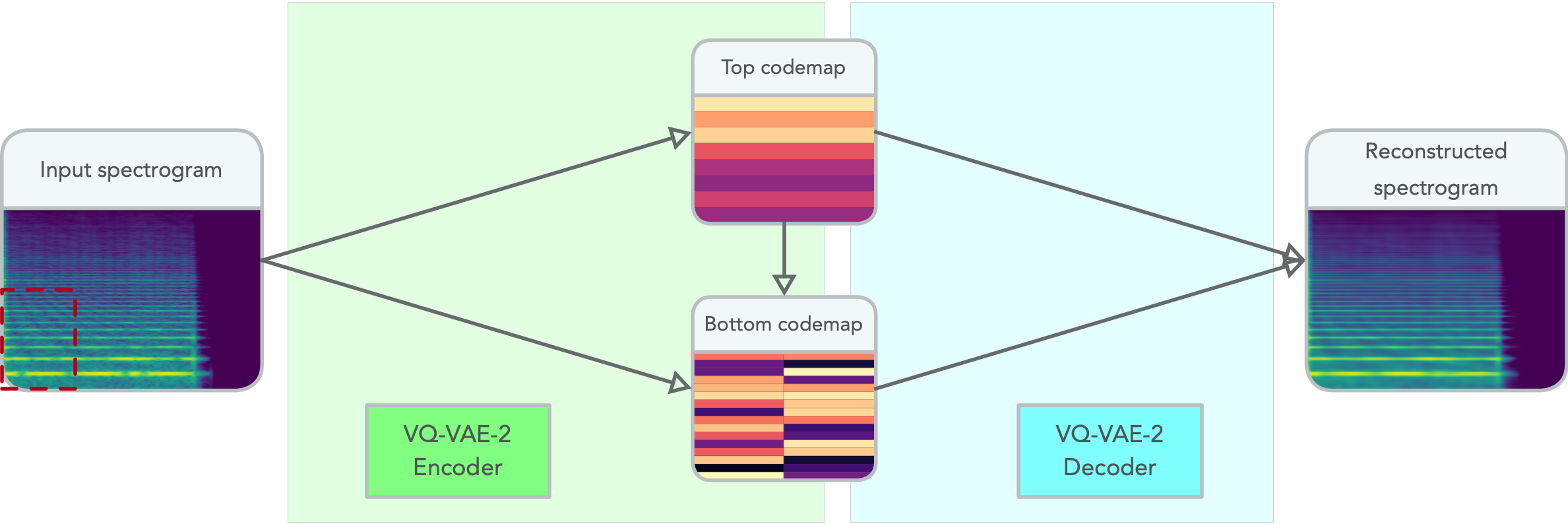
Image-like Representation for Audio
In order to directly apply the VQ-VAE-2 architecture to sounds, we introduce a modified version of the Mel-IF representation used in the GANSynth model, which helps the VQ-VAE-2 learn more robust codes by removing irrelevant noise in the phase at low sound amplitude. We furthermore tweak the Mel-scale to make it “more logarithmic” by lowering the break frequency, resulting in even more resolution in the lower frequencies.
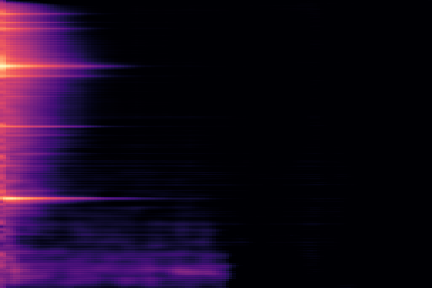
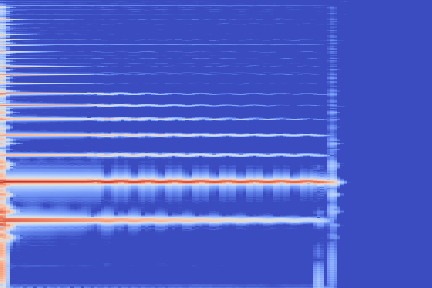
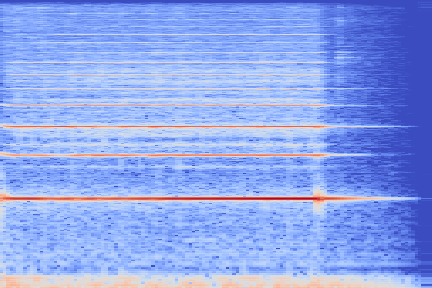
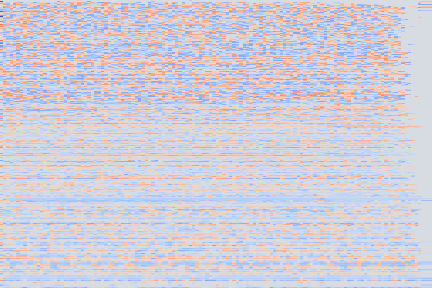
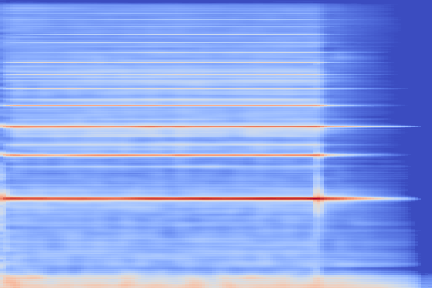
We take the following sound sample as example (sampled from the validation set of our custom NSynth split).
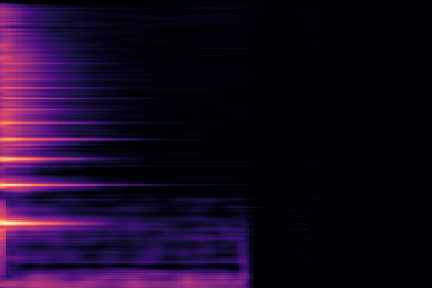
On the following figure, we display the original, GANSynth-style Mel-IF representation for this sound, without phase thresholding and mel-scale compression. We also show the associated top and bottom codemaps obtained from a model trained on this representation.
| Amplitude | IF | |
|---|---|---|
| Original | 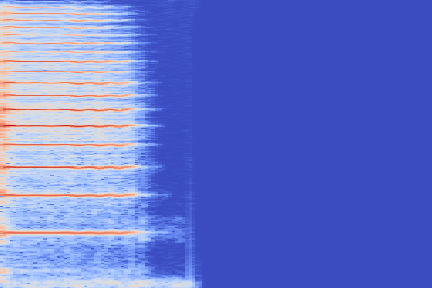 |
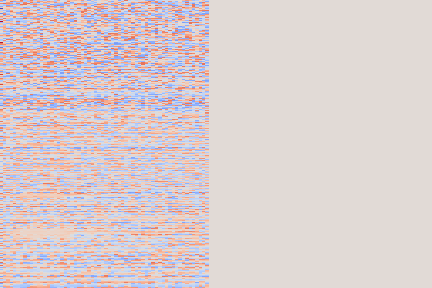 |
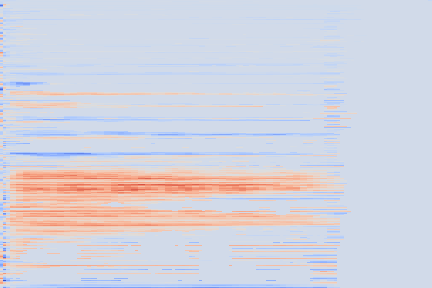
| Reconstruction | 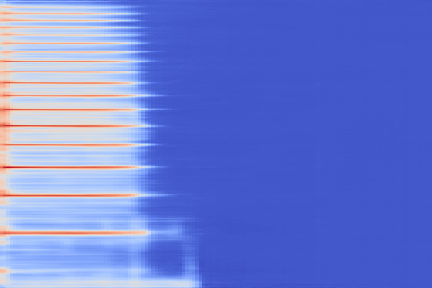 |
 |
| Top | Bottom | |
|---|---|---|
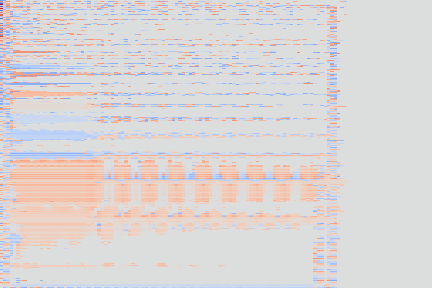
| Codemaps | 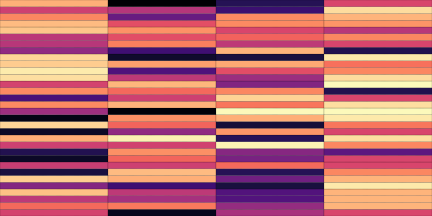 |
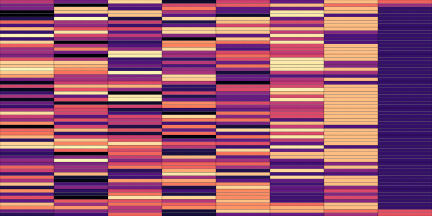 |
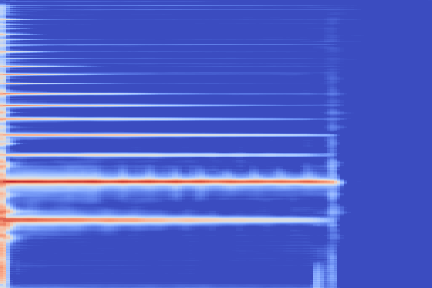
We now show the same spectrogram using our modified representation and the associated codemaps, obtained from a VQ-VAE-2 trained on these representations.
| Amplitude | IF | |
|---|---|---|
| Original | 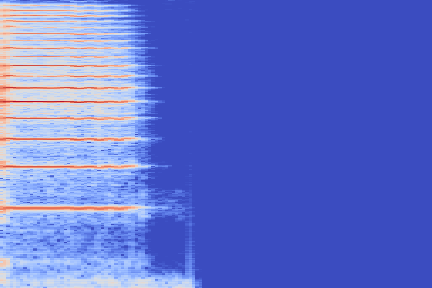 |
 |
| Reconstruction | 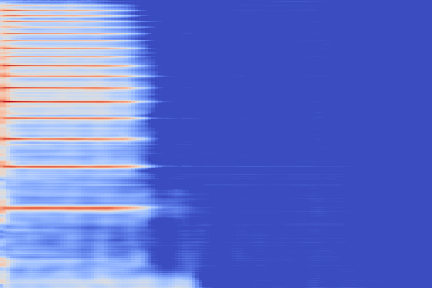 |
 |
| Top | Bottom | |
|---|---|---|
| Codemaps | 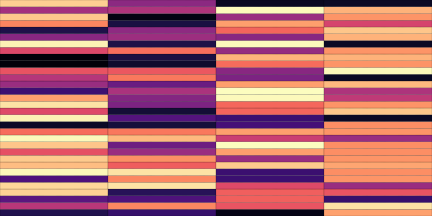 |
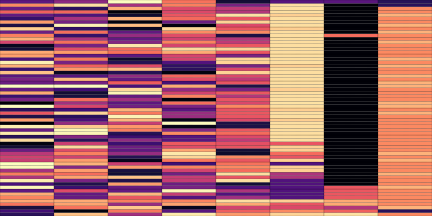 |
Note how the last three columns of the bottom codemap show large homogeneous zones with the same value, the transformation indeed pushed the VQ-VAE to learn a more robust representation where silent zones are assigned the same code.
Sequence-masked Transformers for Inpainting
Sampling new sounds can now be done dy directly sampling from the joint probability of top and bottom codemaps: \[ p(c^{T}, c^{B}) \] This probability can be readily factorized using the classic Bayes-rule into the following product of conditional probabilities: \[ p(c^{T}, c^{B}) = p(c^{T}) p(c^{B} | c^{T}) \]
We model these two probabilities using two distinct autoregressive Transformers. Since we also want to perform inpainting on the generated sounds, that is, resample single tokens in the codemaps for interactive generation, the chosen modeling must allow to account for both the past and future context of each token.
For the top codemaps, we selectively incorporate information from the relevant future tokens using a boolean mask \( m \), the inpainting mask: \[ p(c^{T}) \rightsquigarrow{} { p(c^{T}_i | c^{T}_{<i}, m \odot{} c^{T}_{\geq{}i}) } \]
For the bottom codemap, we perform common autoregressive modeling whilst incorporating conditioning from the top codemap: \[ p(c^{B} \vert c^{T}) = \prod_i{ p(c^{B}_i | c^{B}_{<i}, c^{T}) } \]
The complete inpainting process is represented in this diagram:
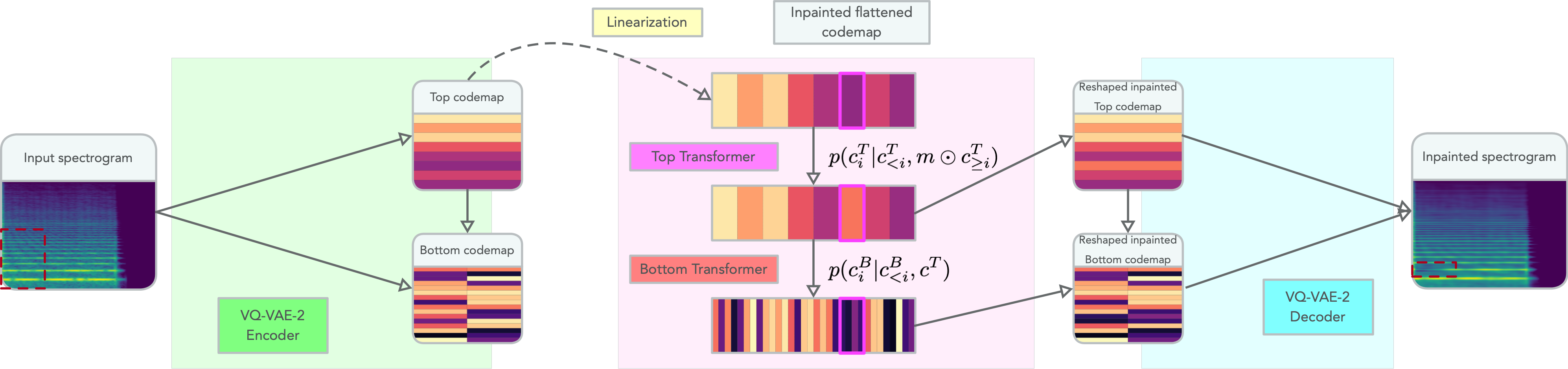
On the right-hand side of this diagram we can see the inpainting procedure in action:
- The codemaps extracted by the VQ-VAE-2 encoder are linearized and fed to the Transformers (see paper for details on the linearization scheme),
- The token circled in pink from the top map is resampled using the conditional probability computed by the top Transformer,
- The underlying tokens in the aligned bottom map are resampled according to the conditional probabilities computed by the bottom Transformers.
- The resulting, inpainted codemaps are decoded back to a spectrogram using the VQ-VAE-2 decoder.
Experiments
We now present audio samples for the different components of our approach.
The models were trained on the NSynth dataset, using a custom 80/20 train/valid split since the original was made across instrument types, which is not relevant for our approach.
VQ-VAE reconstructions
For this first experiment, we only showcase the trained VQ-VAE’s reconstruction ability.
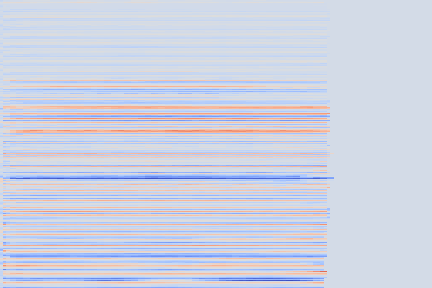
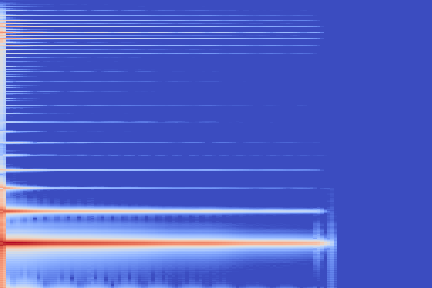
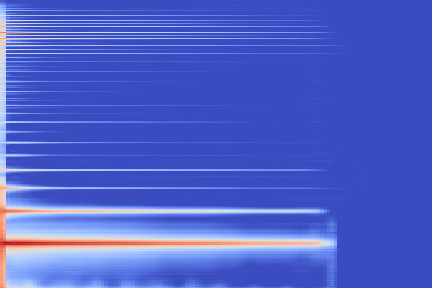
The experimental setup is as follows: we sample 16 random examples from the NSynth validation split and compute their reconstruction using the VQ-VAE-2 encoder. The following (scrollable) table displays the audio and the spectrograms for the original and reconstructed spectrograms. We discuss some noticeable artifacts thereafter, using the highlighted samples as reference.
| Kind + Audio | Mel-Amplitude | Mel-IF |
|---|---|---|
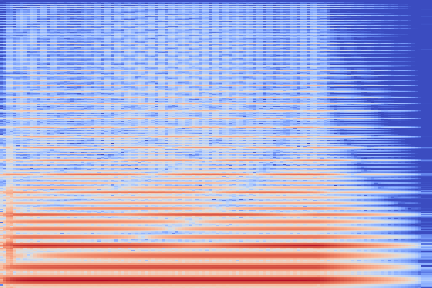
|

|
|

|
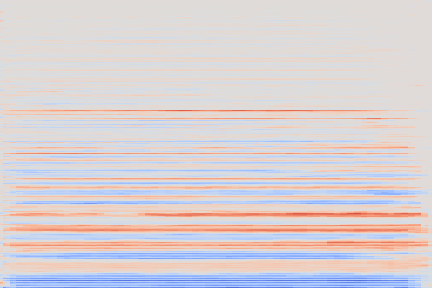
|
|
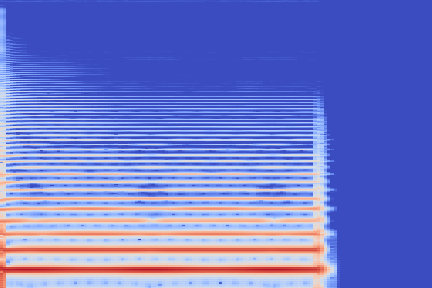
|

|
|

|

|
|
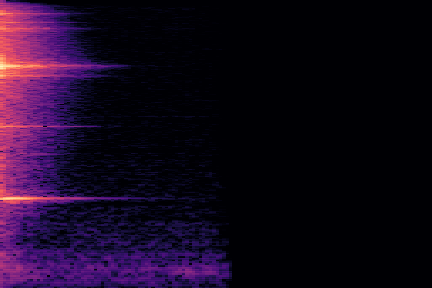
|
|
|
|

|
|

|
|
|
|
|
|
|
|
|
|

|
|

|

|
|

|

|
|

|
|
|

|

|
|

|
|
|
|
|
|
|
|
|
|
|
|

|

|
|

|
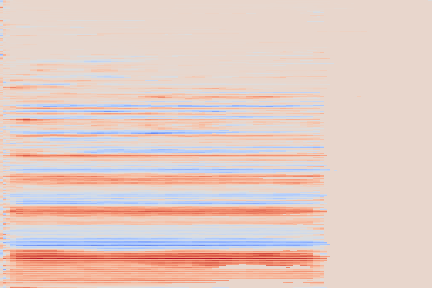
|
|
|
|
|
|
|
|

|

|
|
|

|
|
|

|
|
|

|
|

|
|
|

|

|
|

|
|
|
|

|
|
|

|
|
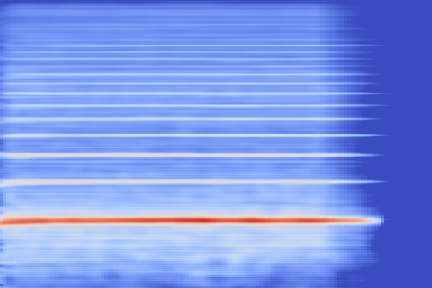
|
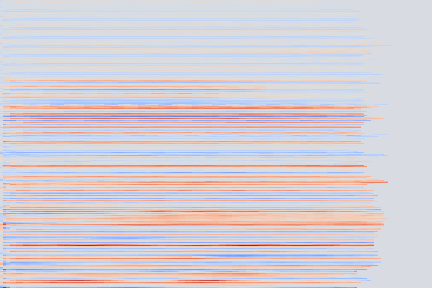
|
Discussion
From these examples we can note that reconstruction with this highly compressed model is good, in the sense the overall timbre is indeed reproduced for each of the samples, yet it is not perfect.
Transients
Transient parts, amongst which attacks, tend to be blurred out, such as in the Keyboard - 78 example, reproduced below.
| Kind + Audio | Mel-Amplitude | Mel-IF |
|---|---|---|
|
|

|

|
|
|

|

|
This is likely cause by the low temporal resolution of the VQ-VAE-2 we employ, where the bottom codemap only operates over frames of duration 0.5 second.
This limitation could be directly tackled by increasing the resolution of the codemaps, but at the cost of increasing the computational load in the subsequent autoregressive modeling by the Transformers.
Another possible solution would be to add a noise component in the VQ-VAE, effectively turning the synthesis process into a harmonics+noise one, as is done in the DDSP model. In this model, the network learns to generate both a set of additive harmonics as well as a FIR filter which is applied on a noise generator to reconstruct noisy components of the input signal. This second technique is grounded in a practice of introducing powerful inductive biases into the architecture of a model in order to ease its learning process.
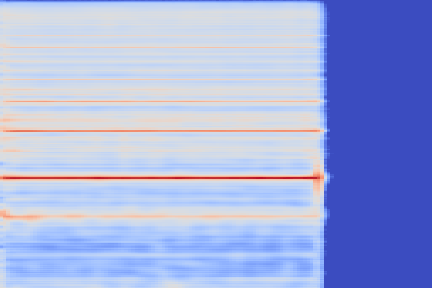
Beating frequencies
Some undesired beating effects appear on sustained notes. An instance of this is in the reconstruction of the String - 68 sample.
| Kind + Audio | Mel-Amplitude | Mel-IF |
|---|---|---|
|
|

|

|
|
|

|

|
This could be due to the reconstructed spectrogram being too smooth to reproduce the complex timbre, leading to this beating artifacts because of missing harmonics.
A first, somewhat brute-force solution would be to increase the network’s capacity, which can be readily done by increasing the codebooks’ size. This would allowing the VQ-VAE to learn a more diverse set of spectral patches, again at the cost of increased computational load.
Notwithstanding, adding a noise component to the model could again help it account for this variability.
Testing these possible enhancements will be the subject of follow-up work.
Unconditional Generation
In this second set of experiments, we make use of the Transformers and evaluate their ability at generating full sounds without receiving any conditioning except pitch and instrument type.
For this sampling procedure, we first autoregressively sample the full top map starting from an initial fully masked self-conditioning map. We then sample the full bottom codemap conditioned on this top map.
Our conditioning scheme for global labels is a very simple one: one-hot encodings (along with a learned embedding matrix) for both pitch and instrument global labels are concatenated to each tokens of the sequences, along with the positional embeddings common in sequence modeling. This simple approach readily gives the networks access to the global conditioning information at all positions. In particular, the global conditioning is concatenated to the start symbols that are prepended to the sequences for autoregressive modeling, allowing to condition the full autoregressive sampling procedure.
| Instrument | MIDI Pitch \(24\) | MIDI Pitch \(31\) | MIDI Pitch \(38\) | MIDI Pitch \(45\) | MIDI Pitch \(52\) | MIDI Pitch \(59\) | MIDI Pitch \(66\) | MIDI Pitch \(73\) | MIDI Pitch \(80\) |
|---|---|---|---|---|---|---|---|---|---|
| Bass | |||||||||
| Brass | |||||||||
| Flute | |||||||||
| Guitar | |||||||||
| Keyboard | |||||||||
| Mallet | |||||||||
| Organ | |||||||||
| Reed | |||||||||
| String | |||||||||
| Synth_lead | |||||||||
| Vocal |
Discussion
The VQ-VAE/Transformer pair successfully handles pitch and instrument conditioning for the diverse set on instruments in the training set.
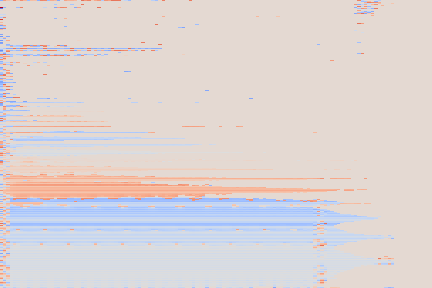
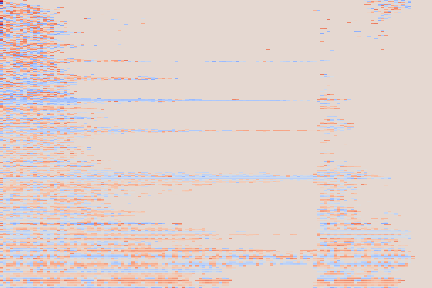
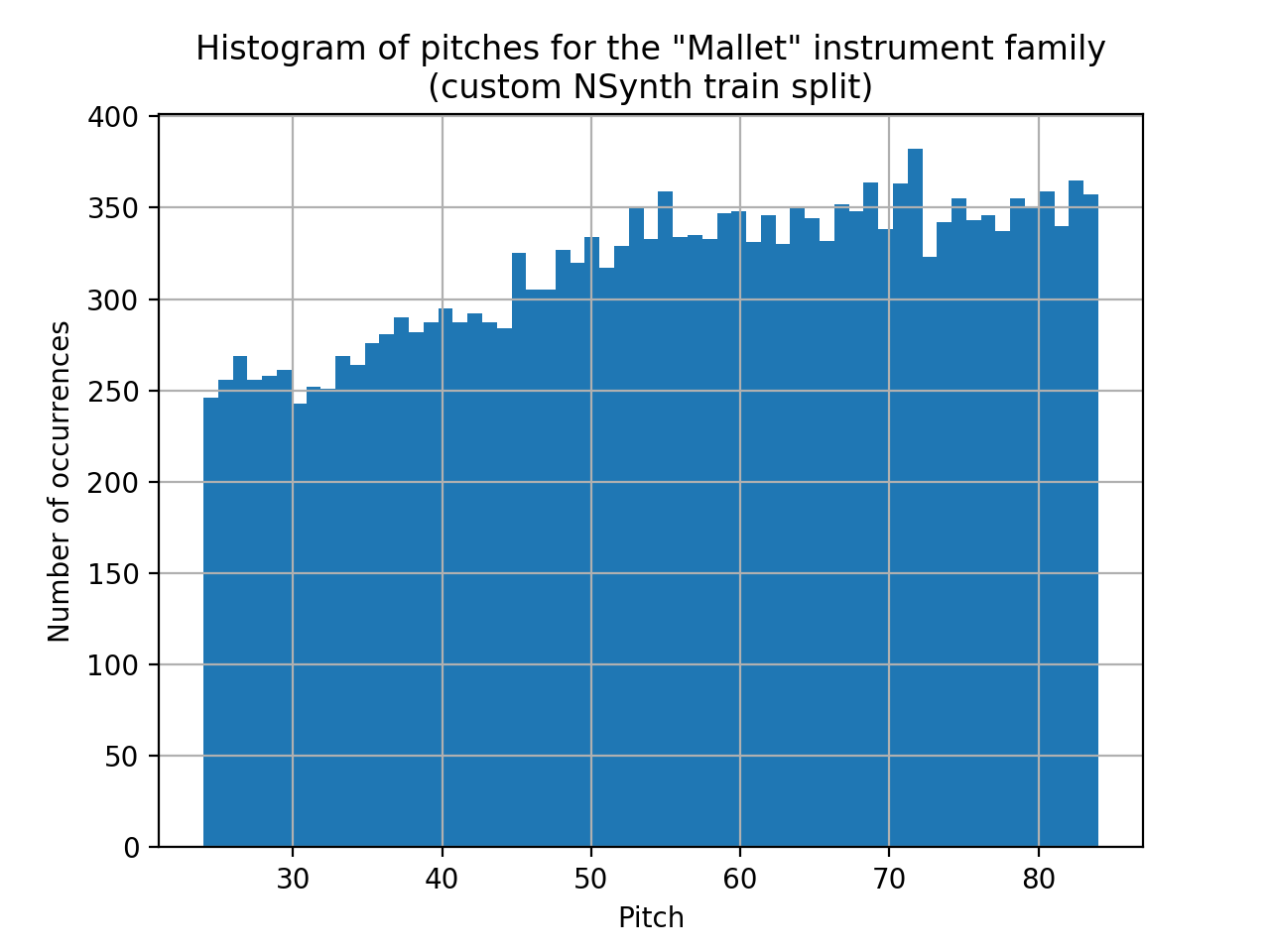
We note that it nevertheless sometimes fails to produce the desired pitch, for instance on the Mallet/24 sample, where the generated pitch is too high. This can be attributed to the fact that pitch 24 is, with 246 occurrences in our train split, one of the least represented pitches for the “mallet” instrument family (as shown on the diagram below). This, along with the fact that our conditioning scheme imposes no disentanglement of the different conditioning modalities, could explain that the networks has a hard time generalizing to this less represented pitch for the given instrument type.
Inpainting operations
We now present some applications of the inpainting capabilities of the masked Transformers. Reviewers are invited to try out these manipulations on the interactive web interface we built for our models, the link of which is to be found in the paper.
Here, we start from a pre-existing sample, either provided by the user or fully generated by autoregressively sampling from the distribution modeled by the Transformers. We then select and resample specific zones in these codemaps, which can be done in a context-aware fashion using the masking procedure introduced in the Transformers.
The two different layers of the VQ-VAE allow to perform sonic transformations at different scales. By editing the top codemap, on which the bottom codemap is, in turn, conditioned, one can perform radical changes on the existing sound.
We perform all our demonstrations on the following sample, taken from the official NSynth test split:
| Audio | Name | Instrument family | Pitch |
|---|---|---|---|
| organ_electronic_028-048-050 | Organ | 48 |
We perform different experiments using all instrument types across a wide range of pitch constraints.
For each combination of pitch and instrument constraints in the following tasks, we sample four independent examples from our models, which are played in succession in the audio files presented.
Temporal inpainting
For this first set of experiments, we regenerate the first two seconds of both the top and bottom codemaps in succession.
This amounts to the following interaction on the interactive interface we propose:
The results are presented in the following table.
| Instrument | MIDI Pitch \(24\) | MIDI Pitch \(36\) | MIDI Pitch \(43\) | MIDI Pitch \(48\) | MIDI Pitch \(60\) | MIDI Pitch \(64\) | MIDI Pitch \(67\) | MIDI Pitch \(72\) |
|---|---|---|---|---|---|---|---|---|
| Bass | ||||||||
| Brass | ||||||||
| Flute | ||||||||
| Guitar | ||||||||
| Keyboard | ||||||||
| Mallet | ||||||||
| Organ | ||||||||
| Reed | ||||||||
| String | ||||||||
| Synth_lead | ||||||||
| Vocal |
Frequency inpainting
In this second set of experiments, we regenerate the lower fourth of both the top and bottom codemaps in succession. This transformation can be used to add bottom-frequency content to a sound. In particular, the bass and organ constraints with a low pitch constraint allow to bring more depth to a sound, as can be heard on the provided examples.
This amounts to the following interaction on our interactive interface:
Note that we restrict the set of constraint pitches to only the lower ones, relevant to this inpainting task.
| Instrument | MIDI Pitch \(24\) | MIDI Pitch \(36\) | MIDI Pitch \(43\) | MIDI Pitch \(48\) |
|---|---|---|---|---|
| Bass | ||||
| Brass | ||||
| Flute | ||||
| Guitar | ||||
| Keyboard | ||||
| Mallet | ||||
| Organ | ||||
| Reed | ||||
| String | ||||
| Synth_lead | ||||
| Vocal |
Keep the top, regenerate the bottom
In this third and last set of experiments, we keep the top codemap unchanged and regenerate the full bottom codemap conditioned on it. According to the hierarchical structure of the model, this can be expected to transform the timbre of the sound without changing its overall envelope and structure.
This amounts to the following interaction on our interactive interface:
The following table contains the resulting sounds for this set of inpainting operations.
| Instrument | MIDI Pitch \(24\) | MIDI Pitch \(36\) | MIDI Pitch \(43\) | MIDI Pitch \(48\) | MIDI Pitch \(60\) | MIDI Pitch \(64\) | MIDI Pitch \(67\) | MIDI Pitch \(72\) |
|---|---|---|---|---|---|---|---|---|
| Bass | ||||||||
| Brass | ||||||||
| Flute | ||||||||
| Guitar | ||||||||
| Keyboard | ||||||||
| Mallet | ||||||||
| Organ | ||||||||
| Reed | ||||||||
| String | ||||||||
| Synth_lead | ||||||||
| Vocal |